Technical FAQ: Why do my three bikes handle differently?

Dear Lennard,
I’ve never quite understood how fork angle, fork offset, and the resulting trail affect the way a road bike feels and steers. In my life, I’ve had three racing bikes with these three very different front ends, and I thought if you could tell me what the numbers mean to you, it might help me and your other readers understand bike geometry a little better.

1. 73-degree fork angle with a 40mm offset and a 110mm stem.

2. 74-degree fork angle with a 45mm offset and a 90mm stem.

3. 72.5-degree fork angle with a 49mm offset and a 90mm stem.

All three felt solid at speed. No. 1 felt good until I got No. 2. With No. 2, I felt like I could just lean the bike and it would turn itself, which No. 1 did not. No. 3, my latest bike, doesn’t feel quite as intuitive going into the turns, but once in the turn, it feels the most rock-solid of them all. (It’s laterally the stiffest by far, which may be factor.) The only other comment I have is that the steering for No. 3, which is rock-solid at high speed, feels surprisingly loose at low speeds. I can’t recall feeling that with my first two bikes.

When you look at numbers like that, what do you see in terms of the design? Does any of what I felt make sense? My impression is that steeper angles, more offset, and longer stems all increase the “quickness” of the steering, but I’m sure it’s much more complex and interesting than that.
— Steve

[related title=”More Technical FAQ” align=”right” tag=”Technical-FAQ”]

Dear Steve,
This is a complicated question with lots of variables involved, some of which you’ve identified. I have an entire chapter devoted to this subject in my Zinn’s Cycling Primer book. In it, I have a way that you can demonstrate to yourself with your own bike what happens when you change its head tube angle (what you refer to as “fork angle”).

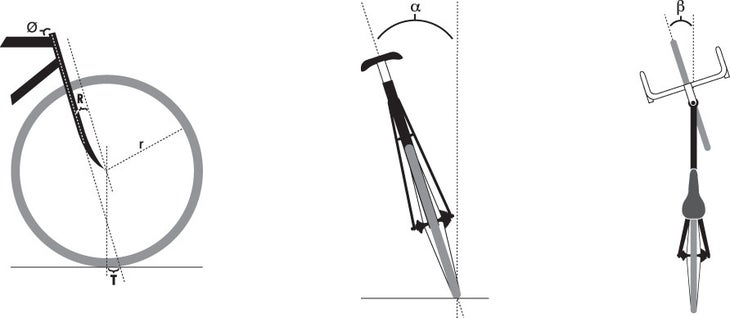
To answer your questions, we have to first define some terms. Fork rake (a.k.a. “fork offset”), “R,” is the perpendicular distance from the center of the front hub to the steering axis. Fork trail, “T,” is the horizontal distance between the center of the tire contact patch on the ground and the intersection of the steering axis with the ground. Head angle, “Ø,” is the acute angle between the steering axis and the horizontal. The wheel radius is “r.”

On most bikes, the steering axis intersects the ground ahead of the tire’s contact with the ground, hence, the tire contact “trails” the steering axis, even though it’s out in front of the bike. This is the same situation as a shopping cart caster, in which the “trailing” of the wheel is more obvious. In that case, when you pull one cart out of the stack of shopping carts, the little front casters flip around away from you so that their little forks are pointed forward. Then when you push the cart forward, those little forks flip around and point backward, toward your feet. The steering axis, or the axis about which each caster’s fork spins, is vertical; if it were not, the front end of the cart would go up and down whenever the fork flipped around one way or the other.

Whether you are pushing or pulling the shopping cart, its little front forks flip around so that the contact point of each caster is behind the steering axis relative to the direction of travel of the shopping cart. In other words, the front casters always “trail” the cart in its direction of motion, which allows you to easily steer it. Each caster’s trail, T, is the distance the center of the caster’s contact patch is behind the intersection of the vertical steering axis.

I like to think of a bicycle’s fork trail as the lever that rights the bike; one way to increase a bike’s stability is to increase the fork trail. Trail, T, is related to the above variables by this expression:

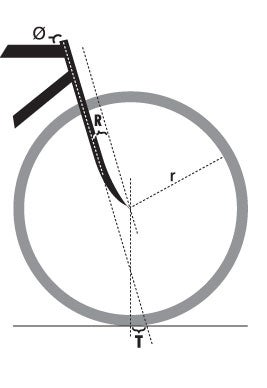
T = (r cosØ – R)/sinØ

You can see from this equation, as well as from looking at a bike, that increasing fork rake (offset) without changing head angle or wheel radius results in a decrease in fork trail (and, hence, reduced stability). You can also see that increasing the head angle (i.e., making the head tube steeper) without changing fork rake (offset) or wheel radius also results in a decrease in fork trail (and, hence, reduced stability). Finally, you can see that increasing the wheel radius without changing fork rake (offset) or head angle results in increased fork trail (and, hence, increased stability).

I’m assuming that the wheel radius is constant on your three bikes, so they have the following amounts of fork trail:

1. 73-degree head angle/40mm offset = 63mm trail

2. 74-degree head angle/45mm offset = 51mm trail

3. 72.5-degree head angle/49mm offset = 57mm trail

My interpretation of your description of your riding impression is that bike No. 2 has quicker-steering than bike No. 1. That is quite obvious from its much smaller-magnitude fork trail.

Good bike design requires balancing steering quickness with stability. An example of a bike that is very stable would be a Harley motorcycle, which has a super long fork with the wheel way out in front, because the head angle is so low. That low head angle, coupled with low fork rake (offset), gives it an enormous amount of fork trail and enormous stability. But it is very much lacking in maneuverability. Similarly, you can make a bicycle super stable by turning the fork around backward (like on a stayer’s bike on the track, where the speeds behind the motorcycle are high, and the banking eliminates the need for maneuverability), but its handling would be sluggish, because its super-high fork trail would make it too stable to be steered easily.

Your bike No. 3 would again be more stable than your bike No. 2, as it has higher fork trail. And its “loose” feeling at low speeds is related to its higher “wheel flop.” In other words, a bicycle’s front wheel flops further into the lean based on the above variables. To see it, stand next to your stationary bicycle and lean it over to one side; the wheel will not stay in the same plane as the bike. Rather, it will flop further into the lean.

The greater the fork trail, the more it will flop into the lean. Conversely, if the fork trail is negative, which can be achieved with a steep head angle and a huge amount of fork rake (bikes don’t exist with negative trail; you would have to make one), when you lean the bike over, with weight on it, the front wheel will instead turn the opposite direction — out of the direction of the lean. This is the definition of an unstable bike!

It may surprise you that the wheel of a more stable (higher-fork-trail) bike would flop over more, into the turn, than the front wheel of a quick-steering (less stable, lower-fork-trail) bike would. You may assume that the wheel flops further into the lean to make the bike turn faster, but that is not the case. The front wheel of the more stable bike flops over more quickly to get the tire contact patch back under the rider’s center of mass more quickly and hence, bring the leaning rider back out of the lean and back to upright more quickly.

The amount of wheel flop is given by this equation:

Wheel flop = cosØ * sinØ * T

Here is the magnitude of wheel flop of your three bikes:

1. 73-degree head angle/40mm offset/63mm trail = 18mm wheel flop

2. 74-degree head angle/45mm offset/51mm trail = 14mm wheel flop

3. 72.5-degree head angle/49mm offset/57mm trail = 16mm wheel flop

The greater wheel flop of bike No. 3 relative to bike No. 2 gives it the more “loose” feeling you describe at low speeds. This is the reason that I would make a bike with less wheel flop for an elderly rider who rides very slowly. It would seem counter-intuitive, because in order to do it, I would be making the bike less stable at speed by virtue of its reduced fork trail. But elderly riders tend to ride slowly, they don’t tend to counter-steer (see below), and they don’t like the feeling of the bike zigging back and forth quickly as they lean from one side to the other that a stable (high-trail) bike would tend to provide.

The way to turn a stable bike (i.e., one with high fork trail, like your bike No. 1) quickly and powerfully on a road with good traction is by counter-steering, which takes advantage of the inherent stability of the bike — the tendency of the front wheel to try to get back under the rider’s center of mass. Everybody counter-steers unconsciously to a certain extent, but few understand it well enough to take advantage of its tremendous power. I also have a chapter on counter-steering in Zinn’s Cycling Primer, and I have written about it in the print version of VeloNews and in this online column over the years.

If you watch cornering motorcycle road racers, who are riding stable bikes at high speed on road surfaces with good traction, you will see that the inside arm is much straighter than the outside arm as they counter-steer and push the bike down into the lean by pushing forward (and down) with their inside hand (and even may be pulling back with their outside hand). You dive into a sharp lean in a corner by pushing the contact patch of the front tire out from under your center of mass with this counter-steering pressure; the inherent stability of the high-trail bike will constantly work against your counter-steering pressure by trying to turn the fork further into the lean to get the tire contact patches back under your center of mass.

As for your comment about stem length, there are more variables there than you may be considering, like your weight distribution over the wheels, particularly the amount of mass supported on the front wheel. A longer stem actually deadens responsiveness a bit, because the same movement at the handlebar results in less angular rotation of the fork. The fact that your most stable bike (bike No. 1) had the longest stem would tend to be another variable resulting in reduced responsiveness, which I think is what you are describing with respect to this bike.

That should answer your questions. It’s probably more than you expected, but that’s what it took to fully answer them!
― Lennard